幻の粒子「マヨラナ粒子」の発見 ―トポロジカル量子コンピューターの実現に期待―
京都大学
東京大学
東京工業大学
概要
京都大学大学院理学研究科の笠原裕一 准教授、松田祐司 同教授、大西隆史 同修士課程学生(研究当時、現:富士通株式会社)、馬斯嘯 同修士課程学生、東京大学大学院新領域創成科学研究科の芝内孝禎 教授、水上雄太 同助教、東京大学大学院工学系研究科の求幸年 教授、東京工業大学理学院の田中秀数 教授、那須譲治 同助教、東京大学物性研究所の杉井かおり 研究員らの共同研究グループは、蜂の巣状の平面構造をもつ磁性絶縁体の塩化ルテニウム(α-RuCl3)において熱ホール効果(注1)が量子力学で規定される普遍的な値をとることを発見し、「マヨラナ粒子(注2)」を実証することに成功しました。マヨラナ粒子は自分自身がその反粒子(注3)と同一という不思議な性質を持ち、理論的予言から80年以上もその存在の確証が得られていなかった「幻の粒子」です。素粒子物理学を中心に探索が続けられてきましたが、近年、ある種の超伝導体や磁性体でマヨラナ粒子が出現する可能性が指摘され、大きな注目を集めてきました。本研究により、マヨラナ粒子が存在する決定的な証拠が得られただけでなく、マヨラナ粒子による量子化現象が高い温度で実現することが明らかになりました。マヨラナ粒子の制御法の開発を行うことで、高温でも動作可能なトポロジカル量子コンピューター(注4)への応用が期待できます。
本成果は、2018年7月12日に英国の科学雑誌「ネイチャー(Nature)」にオンライン掲載されました。
背景
物質を構成する陽子や電子はフェルミ粒子と呼ばれ、通常反粒子が別の粒子として存在します。例えば、電子の反粒子は陽電子であり、異なる符号の電荷を持つためこれらは別の粒子と見なせます。一方で、粒子と反粒子が同一という特異な性質をもつ中性のフェルミ粒子が、素粒子の一つとして1937年に予言され、マヨラナ粒子と呼ばれています。現在のところ、ニュートリノがマヨラナ粒子の候補とされていますが、素粒子物理学の実験では未だに確認されていません。最近になって、マヨラナ粒子がある種の超伝導体や磁性体中で準粒子(注5)として現れる可能性が指摘され、大きな注目を浴びるとともに強い期待が持たれています。その理由は、マヨラナ粒子は非アーベル量子統計(注6)と呼ばれる特殊な統計に従いますが、この性質を用いることで、環境ノイズに対して強く量子情報を安定に保つことができる、トポロジカル量子コンピューターを実現できると考えられているからです。これまで主に超伝導体の研究から、マヨラナ粒子を観測したという実験結果はいくつか報告されているものの、決定的な証拠が得られたとは言い難く、論争が続いています。そのような中、最近、新しい物質系として磁性絶縁体が注目されています。その契機となったのはキタエフ模型(注7)と呼ばれる理論模型の提案です。通常の磁性体では温度を下げてゆくと、磁性を担う電子スピン(注8)は同じ向きに整列し磁石となりますが、この模型では絶対零度においてもスピンは整列せず量子スピン液体(注9)状態と呼ばれる状態が現れます。この量子スピン液体状態の特筆すべき点は、電子スピンが複数のマヨラナ粒子に分裂する(図1)ことにより、トポロジーによって保護(注10)された量子状態が実現することです。最近、このようなキタエフ模型の候補物質がいくつか見つかってきました。
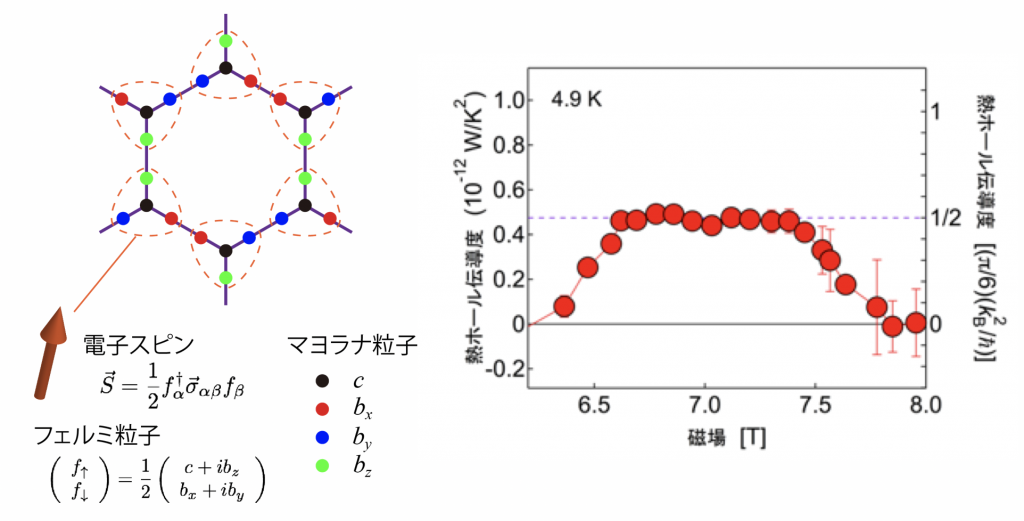
(右)α-RuCl3の熱ホール伝導度の磁場依存性。磁場を変化させると、ある磁場範囲で熱ホール伝導度が量子化熱伝導度(= (π/6)(kB2/ħ))の1/2倍で一定となり、半整数量子化が観測された。
研究手法・成果
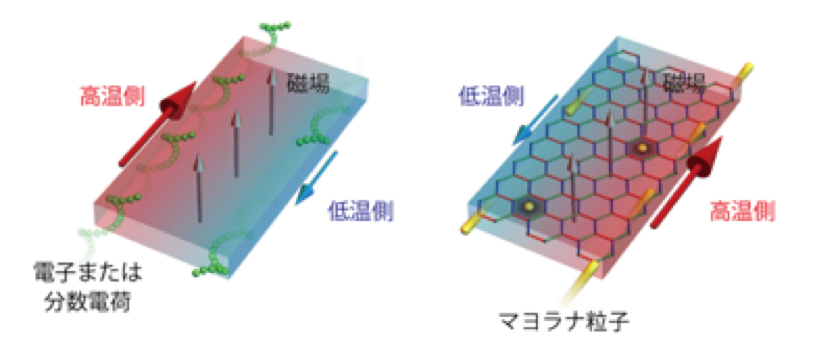
共同研究グループは、キタエフ模型の候補物質である磁性絶縁体α-RuCl3の量子スピン液体状態において、一定の温度下で磁場を変化させながら熱ホール伝導度を非常に高い精度で測定しました。その結果、ある範囲の磁場で熱ホール伝導度が磁場や温度によらずに量子力学で規定される普遍的な値(量子化値)のちょうど半分の値で一定となることを見出しました(図1)。ホール伝導度が量子化値の整数倍または分数倍となる現象は「量子ホール効果(注11)」と呼ばれ、ノーベル賞の対象ともなった二次元電子系における整数量子ホール効果と分数量子ホール効果がよく知られています。このとき、試料の端(エッジ)にはエネルギー散逸がなくトポロジカルに保護された「エッジ流(注12)」 が流れ、整数量子ホール効果では「電子」、分数量子ホール効果では準粒子として現れる「分数電荷」によってエッジ流が運ばれます(図2)。今回、電気が流れない絶縁体において熱ホール効果が量子化していることから、電荷を持たない粒子に由来する量子ホール効果であることが示されます。さらに、熱ホール伝導度が量子化値の1/2倍ということ(半整数量子化)は、熱を運ぶ粒子が電子の半分の自由度を持っていることを示しており、そのような粒子はマヨラナ粒子に他なりません。したがって、整数・分数量子ホール効果に次ぐ「第3の量子ホール効果」を発見したと言えます。半整数量子化は理論的には予言されていたものの観測例はなく、本研究がはじめての実験的証明になります。これまでの超伝導体を用いた研究では、マヨラナ粒子による量子化現象が期待される温度は極低温(1/100ケルビン程度)に限られていましたが、本研究ではそれよりも2桁以上高い温度(5ケルビン程度)で半整数量子化が観測され、高温でマヨラナ粒子にまつわる量子化が出現することが明らかになりました。
波及効果、今後の予定
本研究による半整数量子熱ホール効果の発見の重要性は、理論的提案から80年にわたり探索が続けられてきたマヨラナ粒子の決定的証拠を示しただけでなく、新しい量子凝縮体である量子スピン液体のトポロジカルな性質を証明したという点にもあります。今回対象とした物質のように電子同士が強く相互作用し合う物質(強相関電子系)のトポロジカル物性は未開拓であり、今後の研究の展開により新しい量子現象の開拓が期待されます。さらに、量子スピン液体に現れるマヨラナ粒子の制御法を開発することで、高温でも動作可能なトポロジカル量子コンピューターへの応用が期待できます。
論文タイトルと著者
- タイトル:Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid(キタエフスピン液体におけるマヨラナ量子化と半整数熱量子ホール効果)
- 著者:Y. Kasahara, T. Ohnishi, Y. Mizukami, O. Tanaka, Sixiao Ma, K. Sugii, N. Kurita, H. Tanaka, J. Nasu, Y. Motome, T. Shibauchi, and Y. Matsuda
- 掲載誌:Nature (London)
- DOI:https://doi.org/10.1038/s41586-018-0274-0
- 注1:ホール効果
-
金属や半導体中の電子は磁場下で電磁気学的な力(ローレンツ力)を受けて軌道が曲げられ、電流と垂直方向に電圧が、熱流と垂直方向に温度勾配が生じる。前者を電気ホール効果、後者を熱ホール効果と呼ぶ。電気の流れない絶縁体ではローレンツ力によるホール効果は生じないが、電荷を持たない粒子が熱を運び、熱ホール効果を示すことがある。
- 注2:マヨラナ粒子
-
イタリアの物理学者エットーレ・マヨラナによって1937年に素粒子の一つとして理論的に提案された粒子。
- 注3:反粒子
-
粒子に対し、重さなどの性質は等しいが、電荷など正負の属性が逆の粒子。例えば電子(電荷−e、eは電荷素量)の反粒子は陽電子(電荷+e)である。
- 注4:トポロジカル量子コンピューター
-
0または1の値をとるビットを用いる従来のコンピューターに対し、0と1の量子力学的重ね合わせ状態を取ることができる量子ビットを用いて超並列性を実現できるとされる計算方式は、量子コンピューティングと呼ばれる。トポロジカル量子コンピューターでは系のトポロジー(後述10)を用いて量子情報を保護することで、環境ノイズに対して安定的に量子コンピューティングを行うことが可能になると考えられている。
- 注5:準粒子
-
物質が示す最もエネルギーが低い状態(基底状態)から少しエネルギーを与えた状態は、ほとんど相互作用のない仮想的な粒子が付け加えられた状態としてみなすことができる。このような粒子は「準粒子」と呼ばれ、物質の物理的性質の多くはこの準粒子の性質によって決まる。
- 注6:非アーベル量子統計
-
2つの準粒子を入れ替えたとき、波動関数に1でもー1でもない複素数がかかることがあり、そのような統計性に従う準粒子をエニオンと呼ぶ。2つのエニオンを交換する場合には、交換前後での状態が区別できない場合(可換統計=アーベル統計)と元の状態とは異なる別の状態に変わってしまう場合(非可換統計=非アーベル統計)がある。
- 注7:キタエフ模型
-
基底状態が厳密に量子スピン液体状態を与える蜂の巣状の結晶格子構造をもつ磁性体の理論模型。2006年にアレクセイ・キタエフ(米国カリフォルニア工科大)によってトポロジカル量子計算を実現し得る模型として提案された。
- 注8:電子スピン
-
電子の持つ量子力学的な内部自由度(粒子を区別する性質)のひとつ。その性質は磁石と対応する。
- 注9:量子スピン液体
- 通常、物質の温度を下げると物質を構成する原子や分子が周期的に整列した固体となる。しかし、量子力学的なハイゼンベルグの不確定性原理による量子ゆらぎの影響が顕著な場合、絶対零度まで固体になれずに液体のままでとどまることがある。このような状態は「量子液体」と呼ばれ、液体ヘリウムがよく知られている。量子スピン液体は量子液体のスピン版ともいうべきもので、絶対零度までスピンの向きが揃わず動き回った状態を指す。
- 注10:トポロジーによって保護
-
連続的に変形させても保たれる性質をトポロジー(位相幾何学)と呼ぶ。例えば、取っ手のついたコーヒーカップとボールは穴の数というトポロジーで区別できる状態であり、連続的に移り変わることはできない。この要請により、トポロジカル状態は不純物などの擾乱の影響を受けないという特徴がある。
- 注11:トポロジーによって保護
-
試料に強い磁場をかけたとき、電気ホール伝導度や熱ホール伝導度が、物質の詳細によらず量子化値の整数倍(整数量子ホール効果)または分数倍(分数量子ホール効果)となる現象。量子化電気伝導度、量子化熱伝導度はそれぞれe2/h(電気素量e、プランク定数h)、(π/6)(kB2/ħ) = 9.5×10-13 W/K2(ボルツマン定数kB、ħ = h/2π)である。
- 注12:トポロジカルに保護された「エッジ流」
-
異なるトポロジーで特徴づけられる2種類の物質が接する時、その境界(例えば真空に接するトポロジカル物質の試料端)では擾乱による影響を受けない伝導状態が現れる。